OLIGOPOLY

11.2-1 Introducing Oligopoly and the Prisoner's Dilemma (Warning: this is a long video lecture >20 minutes)

• Outline
  • Oligopoly Defined
  • Game Theory: The Prisoner's Dilemma
  • Nash equilibrium
  • Definition of Dominant Strategy
  • Conclusion
• Oligopoly Defined
  • ERROR: Tomlinson mentions that a monopolistically competitive industry has "a small number of sellers" each with some market power; he meant to say "a LARGE number of sellers".
  • Oligopoly
    • small number of sellers
    • that have to consider the reactions of their competitors;
      • they interact strategically
      • ME: our textbook uses the term "mutual interdependence";
      • where each firm tries to guess what its competitor's are going to do,
      • because the choices of all the firms affects each individual firm
    • there is no generally agreed upon single model of oligopoly: there are several models each with strengths and weaknesses

• Game Theory: The Prisoner's Dilemma
  • economists tend to agree that Game Theory best describes strategic behavior between a small number of firms
  • the Prisoner's Dilemma is one of the most basic forms of game theory and it applies quite will to the strategic behavior of a small number of firms (i.e. oligopoly) when they are making their pricing decisions

   

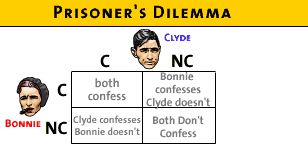
  • Bonnie and Clyde: confess or not confess?
    • called a "game" because the outcome depends not just on what you do, but what your competitor does; also called strategic interaction
    • draw a matrix (table) with two players representing the possible outcomes in each box; prisoners cannot talk to each other and they don't know what the other will choose
      • each can either confess or not confess
      • if both confess they will get 10 years in prison each
      • if neither confess then they will get only 1 year in jail on a lesser charge
      • if Bonnie confesses and Clyde doesn't, then Bonnie is free (no jail time) and Clyde will get 11 years in prison
      • if Clyde confesses and Bonnie doesn't, then Clyde is free (no jail time) and Bonnie will get 11 years in prison
    • Matrix of strategies available to each player:

      

      

       

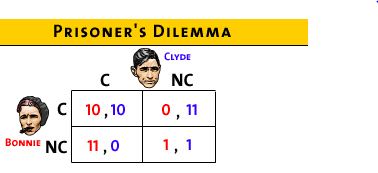
• Nash equilibrium
  • What is the solution?
  • Nash Equilibrium:
    • the outcome when each player is doing the best they can given what all other players are doing
    • If Clyde confesses what is the best response for bonnie?
      • The video lecture will ask you a multiple choice question. ANSWER THE QUESTION by selecting A, B, or C and more of the lecture will follow
    • If Clyde does not confess which is the best response for Bonnie
      • The video lecture will ask you a multiple choice question. ANSWER THE QUESTION by selecting A, B, or C and more of the lecture will follow
    • Definition of Dominant Strategy
      • In both cases, Bonnie will minimize jail time by confessing; this is Bonnie's "dominant strategy"
      • Dominant Strategy: a choice for a player that maximizes her satisfaction no matter what her rivals are doing

        

    • What should Clyde do?
      • The video lecture will ask you a multiple choice question. ANSWER THE QUESTION by selecting A, B, or C and more of the lecture will follow
      • Clyde will also have a dominant strategy of confessing no matter what Bonnie does
    • So they will BOTH confess = Nash equilibrium
      • Nash equilibrium occurs when they both give their dominant response

        

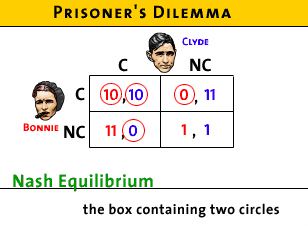
      • it is also a "self-enforcing agreement": when they are each giving their best decision, neither can improve their situation by changing their minds
      • so they will not change their minds; it is an equilibrium
    • BUT is this equilibrium the BEST for Bonnie and Clyde?
      • The video lecture will ask you a multiple choice question. ANSWER THE QUESTION by selecting A, B, or C and more of the lecture will follow
      • It would be best if they would both NOT CONFESS,then they each get only 1 year in prison rather than 10 years
      • but it is not a Nash equilibrium because they can each do better if they confess.
        • they can do better because if one confesses and the other does not then he or she will get no jail time (0 years)
        • so they will confess = Nash equilibrium

        

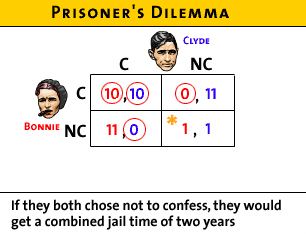
      • The BEST outcome for both is not an equilibrium outcome

     

  • How does this apply to economics and business?
    • businesses try to form trusting relationships so in a situation like this one, no one will be tempted to cheat
    • if Bonnie and Clyde play often enough they may learn to trust one another and both choose not to confess; they can enforce cooperation through trust

      

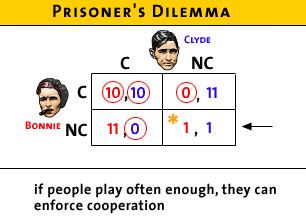
    • but if they only play once, the RATIONAL OUTCOME is for both to confess
      • this is rational even if it isn't the best outcome
    • Maybe they can enforce cooperation other ways:
      • like through third party enforcement of contracts

        

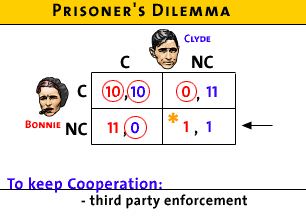
    • but more likely, if people play often enough they can form reputations that they will not cheat; i.e. trust
• Conclusion
  • the best outcome may not be individually rational
    • it would be better for an individual business to pollute (cheaper and therefore larger profits), but it would not best if all businesses polluted
  • how to avoid a Nash equilibrium and end up with the best outcome instead?
    • repeated play
    • reputation
    • contracts

      

     

• NOTE: Tomlinson discusses the next lesson when the prisoners 'dilemma is applied to an oligopoly, I think he is referring to:
  • 10.4-1 Game Theory and Advertising and Brand Names - Understanding Monopolistic Competition as a Prisoner's Dilemma AND this should be titled "Understanding Oligopoly as a Prisoner's Dilemma"

10.4-1 Game Theory and Advertising and Brand Names - Understanding Oligopoly (Monopolistic Competition??) as a Prisoner's Dilemma

11.2-1 should be done before doing this one

• Outline
  • How to use game theory
  • Dominant strategy
  • Prisoner's Dilemma: Best outcomes vs. Actual outcomes
• How to use game theory to understand advertising: Coke and Pepsi
  •  Assumptions:
    • two rivals: Coke and Pepsi competing for a share of the $10 million soft drink market
    • if no advertising they each have $5 million in sales
    • advertising would cost them $3 million
    • if you advertise and your rival does not then you get all customers = $10 million in sales
    • if you advertise AND your rival also advertises then you each get $5 million in sales - the same as if neither advertise
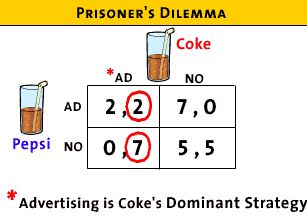
  • Here is the game matrix:
    • 
  • Coke's Dominant strategy
    • The video lecture will ask you a multiple choice question. ANSWER THE QUESTION by selecting A, B, or C and more of the lecture will follow
    • if Pepsi advertises what ts the best strategy for COKE?
      • if Coke does not advertise it will get $0 in sales
      • if coke does advertise it will get $2 million in revenue
      • BEST for Coke to advertise
    • If Pepsi does NOT advertise, what is the best strategy for COKE?
      • if Coke does not advertise it will get $5 in sales
      • if Coke does advertise it will get $7 million in revenue
      • BEST for Coke to advertise
    • So, Coke has a dominant strategy to advertise

      

  • Pepsi's Dominant strategy
    • if Coke advertises what ts the best strategy for PEPSI?
      • if Pepsi does not advertise it will get $0 in sales
      • if Pepsi does advertise it will get $2 million in revenue
      • BEST for Coke to advertise
    • If Coke does NOT advertise, what is the best strategy for PEPSI?
      • if Pepsi does not advertise it will get $5 in sales
      • if Pepsi does advertise it will get $7 million in revenue
      • BEST for Pepsi to advertise
    • So, Pepsi's has a dominant strategy to advertise

      

• Best outcomes vs. Actual outcomes
  • Best outcome:
    • for both Coke and Pepsi is for neither one to advertise and then they each get $5 million revenue

      

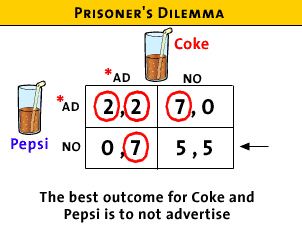
    • but this is NOT a self enforcing agreement because they both will realize that they can now gain by advertising,
      • if they agree together that they will not advertise to achieve their best outcome ($5 million each)
      • one can gain if they advertise (i.e. cheat) if the other one doesn't
      • so it makes sense ("individually rational") to cheat and launch an ad campaign

        

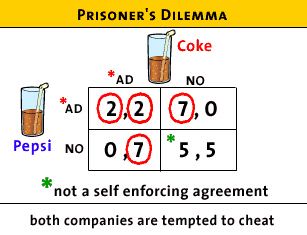
  • But the actual outcome (Nash equilibrium) is that they will both advertise and get only $2 in revenue
    • because the best outcome (5,5) is not a self enforcing agreement
    • but if they both advertise, this is a self enforcing agreement; i.e. they are BOTH giving their best response to their rival

       

• How to get the best (5,5) outcome:
  • they might learn through repeated play that if they both do not advertise that they will both come out ahead
  • or if they can get the government to outlaw soft drink advertising (they would like and support such a law)

    

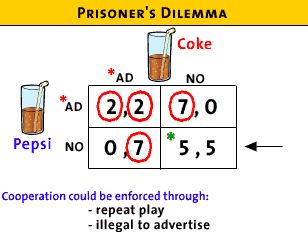
• Prisoner's Dilemma:
  • advertising is like the arm's race (nuclear weapons)
  • it would be best if no one advertises (or had nuclear weapons)
  • but, because of the possibility of your rival doing it, you have to keep up
  • in the end everyone's profits are reduced (2,2)

     

11.3-1 Understanding a Cartel as a Prisoner's Dilemma

11.2-1 should be done before doing this one

• Outline
  • Definition of a Cartel
  • Prisoner's Dilemma
  • Best Outcome

   

• Definition of a Cartel
  • an oligopoly where the individual members try to act as a monopolist
  • ME: (from the textbook) a group of producers that typically creates a formal written agreement specifying how much each member will produce and charge. Output must be controlled—the market must be divided up—in order to maintain the agreed-upon price. The collusion is overt, or open to view.
  • they get together and act as one, setting the price and quantity together, choosing the profit maximizing monopoly quantity and price and earning monopoly profits that they divide among themselves; i.e. they act as a monopoly
  • ME: usually this is done by all member restricting quantity and raising the price
  • Problem: keeping the cartel together is a problem because of the prisoner's dilemma
    • .if one firm knows that all the others are restricting the quantity which makes the price higher, this firm can CHEAT and produce more and make greater profits for itself; i.e. they have an incentive to cheat
    • but if all firms or countries) cheat by producing more, the price will drop and they will all earn lower profits than if no one cheated
• Prisoner's Dilemma: The Cartel as a case of the Prisoner's Dilemma
  • two countries form an oil cartel, Nigeria and Venezuela
  • they each have two options: cooperate or cheat
    • if they both cooperate they earn maximum profits that are shared ($10 million total or $5 each)
    • if both cheat and increase their output then the price will fall an total profits will fall (to $8 million) and they will each earn only $4.
    • if one cheats and produces more but the other does not an still produces less, the cheater more profits ($6) ,but the other makes less profits ($3) and total profits will be less ($6 + $3 = $9) because the price will be lower; i.e. they are not earning the highest, monopoly, profit.

      

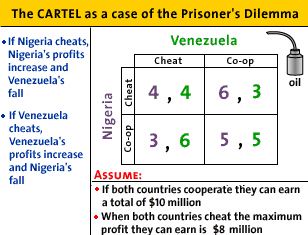
  • What are Dominant Strategies?
    • For Venezuela:
      • if Nigeria cheats, then Venezuela's best response is to cheat also and profits are 4,4.
      • if Nigeria cooperates then Venezuela's best response is to cheat and profits are 3 for Nigeria and 6 for Venezuela
      • So, Venezuela has an incentive to cheat no matter what Nigeria does

        

    • For Nigeria:
      • if Venezuela cheats, then Nigeria's best response is to cheat also and profits are 4,4.
      • if Venezuela cooperates then Nigeria's best response is to cheat and profits are 3 for Venezuela and 6 for Venezuela
      • So, Nigeria has an incentive to cheat no matter what Venezuela does
  • Nash Equilibrium
    • since both countries have a dominant strategy to cheat the Nash equilibrium is for both top cheat and the cartel falls apart
    • profits are $4 million each
    • total profits are at the lowest of all possible options
    • ME: but this is the best outcome for consumers!

      

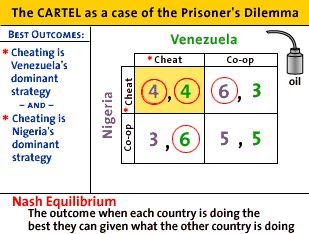
• Best Outcome
  • the best outcome for the oil producing countries is to collude (form the cartel) reduce output, and raise the price acting like a monopolist
  • this way each country would earn profits of $5 million (5,5)

    

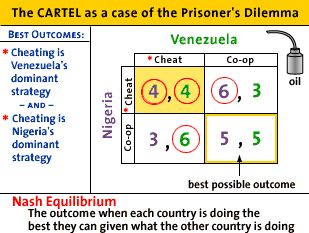
  • but this is not a self enforcing agreement because they each have an incentive to cheat and try to improve their profits
  • so this is not a Nash equilibrium (i.e. not a stable outcome)
• So, what does this mean about cartels? Are they possible?
  • Yes, if they learn through repeated play that cheating hurts them both and that cooperating is better for them.

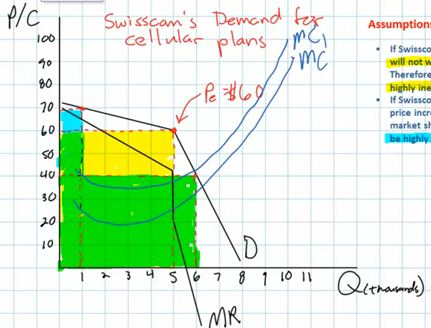
"Kinked Demand Curve Model" for $1.98: at: http://mindbites.com/lesson/7742-economics-kinked-demand-curve-model

• Outline
  • the kinked demand curve
  • the discontinuous MR curve
  • finding the profit maximizing quantity
  • problems with the kinked demand model
• ME: mutual interdependence
• assume:
  • that rivals ignore if one firm raises its price
  • but rivals will match the price change if one firms decides to lower its price
• result: the demand curve will be kinked
  • it will be more elastic (flatter) above the original price because if one firm lowers its price AND all of its competitors do not, then the firm will lose A LOT of customers
  • the demand will be less elastic (steeper) below the original price because if one firm decides to lower its price all of its competitors will ALSO lower their prices and each would get only A FEW new customers
• what will the MR curve look like?
  • as always (except pure competition) the MR will be below the demand curve (D)
  • it will be discontinuous
• how to find the profit maximizing quantity
  • as always, we find the profit maximizing level of output at the quantity where MR = MC
  • It is quite likely that the MC curve will cross the MR curve in the vertical gap
  • if so, then the profit max quantity is found on the horizontal axis directly below the gap and the price is found off of the demand curve above
  • the price would then be at the kink in the demand curve
• Problems
  • one problem with the model is that it does not tell us how the kink in the demand curve got where it is in the first place
  • also there are not many good real world examples
• But, logically it does make sense.

Kinked Demand Model (econclassroom.com 14:06)
http://www.econclassroom.com/?p=3144

Preview:

• In this lesson we take a graphical approach to oligopoly, and seek to explain why prices tend not to fluctuate up or down in oligopolistic markets.
• Why do some oligopolies have very little incentive to decrease their prices, and also a strong incentive not to raise their prices?
• What emerges is a kinked demand curve, highly elastic at prices above the current equilibrium and highly inelastic at prices below the current equilibrium. Along with this kinked demand curve comes a kinked marginal revenue curve, with a vertical section. The implication is that even as an oligopolist's costs rise and fall in the short-run, its level of output and price tends to remain stable.

Review - Oligopolies:

• few firms
• mutual interdependence
  • Mutual interdependence exists when firms consider their rivals' reactions while adjusting prices and outputs.

Assumptions about oligopoly pricing behavior (kinked demand model)

• before changing its price an oligopolist will try to predict what its competitors will do if they do change their price

• ASSUME: competitors will match price decreases - if one firm lowers its price the competitors will lower their prices
  • This make sense because the competitors will not want to lose a lot of customers to a competitor that lowers it price, so they will decrease their price too.
  • therefore, the demand curve is inelastic, if all firms lower their prices they will not gain very many customers, i.e. the % change is quantity demanded will be small = inelastic
• ASSUME: competitors ignore price increases - if one firm raises its price the competitors will not raise their prices
  • This makes sense because competitors could gain a lot of customers if they kept their prices low when one firm raises theirs
  • therefore, the demand curve will be elastic, if one firm raises its price and the other firms do not, the one firm will lose a lot of customers, i. e. the % change in quantity demanded will be large = elastic

So what does the demand curve look like with these assumption?

• demand below the going price will be inelastic (steeper); a small increase in quantity if the price is decreased
• demand above the going price will be elastic (flatter); a large decrease in quantity if the price is increased
• so the demand curve will be "kinked", or bent.

  

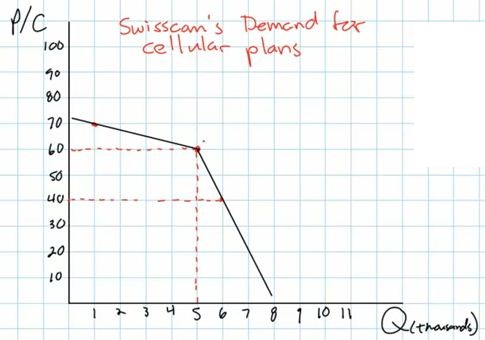
So why are firms reluctant to change their prices?

• since demand is inelastic below the going price, if a firms lowers its price (and its competitors do not) then its total revenues will decrease; a big drop in price but a little increase in quantity causes TR to decline
• since demand is elastic above the going price, if a firm raises its price (and all its competitors raise their prices too) then its total revenues will decrease; a little increase in price but a large decrease in quantity causes TR to decline
• Therefore, prices in an oligopolistic market are "sticky"; i.e. they tend not to change because if a firms raises, or lowers its price, its total revenues will fall

So what does the MR curve look like?

• We know that when the demand curve is downward sloping, the MR curve is below it
• the MR diminishes at twice the rate that demand does therefore, we end up with two MR curves, one somewhat flat under the elastic portion of the kinked demand curve and one more steep under the inelastic portion of the demand curve, and a vertical portion of the MR curve connecting the two

  

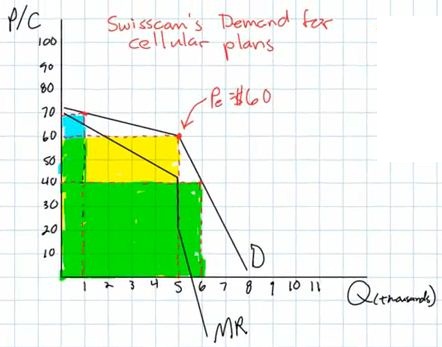
So what will oligopolists do if their costs change? Will they change their prices and quantities?

• maybe not
• in other markets
  • if variable costs rise, the MC will rise and the profit maximizing level of output (where MR=MC) will decrease, and
  • if variable costs fall, the MC will fall and the profit maximizing level of output (where MR=MC) will increase
• but in the kinked demand model, if the MC crosses MR in the vertical section, a change in costs will not change the profit maximizing level of output or the profit maximizing price. the price and quantity where MR = MC will stay the same even if MC rises or falls
  • 

ME:

• Most economic textbook and online video lectures do not include the ATC curve in their kinked demand model. I am not sure why. And they often include 2 MC curves to show that changes in costs do not change the profit maximizing quantity or price.
• here is a graph of the oligopoly kinked demand model with the ATC curve and only one MC:

  

  

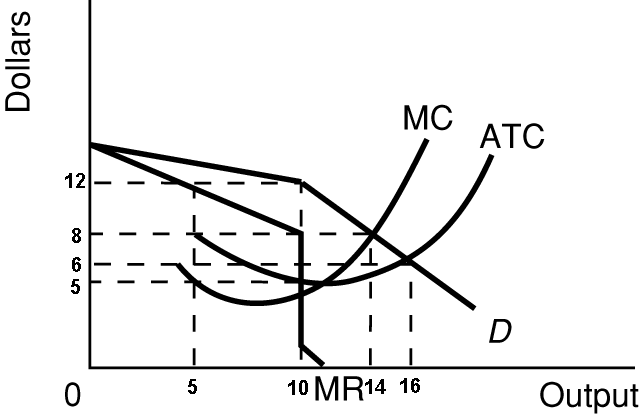
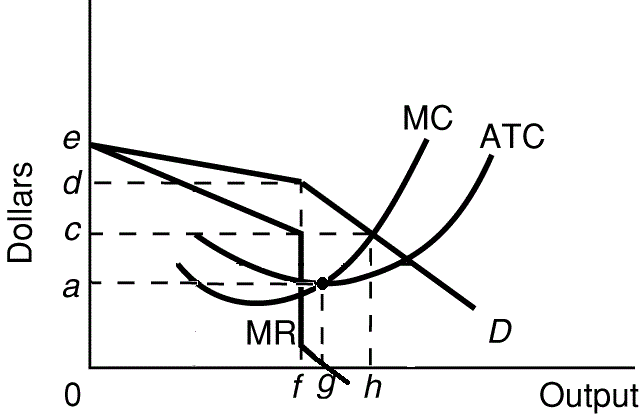
  • Profit maximizing quantity and price: Q = f; P = d
  • Allocatively efficient quantity and price: Q = h; P = c
  • Productively efficient quantity and price: Q = g; P = a

Oligopolies, Duopolies, Collusion, and Cartels (Khan Academy 8:26)
http://www.khanacademy.org/finance-economics/microeconomics/v/oligopolies--duopolies--collusion--and-cartels

Introduction

• oligopoly
  • "oli" means "few"
  • "polies" means "sellers"
• sometimes oligopolies act more like monopolies and sometimes they act more like competitive markets

Collusion (acting more like a monopoly)

• if they coordinate their pricing and production decisions they are acting more like a monopoly
• this is called collusion
• this is often illegal
• if they do it formally (like written agreements) then we call it a cartel
• example of a cartel: OPEC (the Organization of Petroleum Exporting Countries)
  • 12 countries
  • control 79% of the world's oil reserve (2012)
  • and 44% of the world's oil production (2012)
• attempt to act like a monopoly
• one problem with collusion is that individual firms (or countries as in OPEC) have an incentive to CHEAT: i.e. they might be able to make more money if the say that they are going to charge a high price like the rest of the firms, but then they lower their price a take customers away from all the other firms

Oligopolies that are More Competitive

• Example: Coca-Cola vs.Pepsi
• Coke and Pepsi compete on price and on marketing
• a duopoly is an oligopoly with only two major firms
• examples of oligopolies that compete (act more like pure competition):
  • Coca-Cola and Pepsi (duopoly)
  • Boeing and Airbus (large passenger jet manufacturers - duopoly)
  • Airlines
    • most cities have only a few airlines
    • their products are very similar (standardized?)
    • credit card (Visa, Mastercard, Discover American Express)
• governments try to assure that oligopolies compete rather than collude because collusion is inefficient (like monopolies) and when they compete they are more efficient (more like pure competition) with a larger consumer plus producer surplus (total surplus).

SUMMARY

Determining the Efficiency of Firms in Different Market Structures (econclassroom.com 18:23)
http://www.econclassroom.com/?p=4456

Introduction

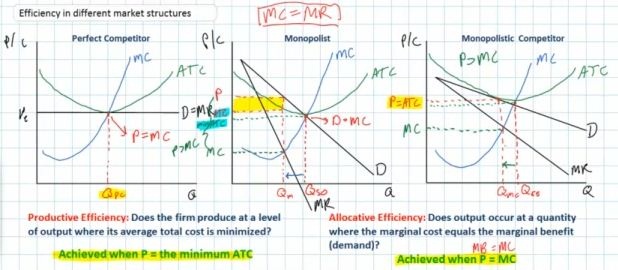
• two types of efficiency
  • productive efficiency
    • producing at the level of output where its ATC is minimized
    • is the price equal to the minimum ATC
    • ME: quantity where MC=ATC
  • allocative efficiency
    • producing at the level of output where the MB = MC
      • ME: MSB = MSC
    • achieved where P=MC (or D=MC)
    • the demand curve represents the MB that consumers receive from the consumption of a good
    • also called the socially optimal quantity
    •  

Perfect Competition Long Run Equilibrium

• very many firms producing standardized (identical) products with no barriers to entry
• demand perfectly elastic (firm is a price taker) since there are very many firms producing identical products and no individual firm has any market power
• D=P=MR
• equilibrium price is established in the market (supply and demand in the market)
• zero (normal) economic profits in long run equilibrium because of no barriers to entry so ATC touches demand at the lowest point of the ATC curve
• quantity produced is where MR=MC (Qpc)
• productive efficiency is achieved
  • equilibrium quantity (Qpc) is where ATC is at a minimum (P=minimum ATC)
  • produce the quantity where MC=ATC
  • if they produce at any other quantity then the ATC will be greater than the price and they will earn economic losses and will go out of business in the long run
• allocatively efficiency is achieved
  • at the profit maximizing quantity (Qpc) the P=MC
  • MSB=MSC
  • this is the socially optimal quantity

  

Monopoly Long Run Equilibrium

• single firm in the industry since entry is blocked
• producing a unique product
• downward sloping demand since the monopolist has market power since it produces a unique product that no other firms produce and the demand (or P) is greater then the MR
• D=P>MR
• long run profits likely shown on graph as the ACT is below the demand (P) curve because entry is blocked (yellow rectangle)
• quantity produced is where MR=MC (Qm)
• productive efficiency is NOT achieved
  • equilibrium quantity (Qm) is NOT where ATC is at a minimum (P>minimum ATC)
  • they do NOT produce the quantity where MC=ATC
  • at the profit maximizing level of output (Qm) the actual ATC is higher than the minimum ATC
  • since there is no competition the firm does not need to produce in the least cost manner; without competition the firm can charge a much higher price and produce at a higher ATC and earn greater profits
• allocative efficiency is NOT achieved
  • equilibrium quantity (Qm) is NOT at the quantity where P=MC (Qso)
  • at the profit maximizing level of output (Qm), P>MC
  • meaning that there is an underallocation of resources; too little is being produced
  • monopolists can restrict output to increase the price and earn greater profits
  • at the socially optimal (alloc. eff.) quantity (Qso), profits are not maximized so the monopolist will not produce this quantity

  

Monopolistic Competition Long Run Equilibrium

• many firms in the industry producing similar products
• some market power (price making power) because of product differentiation
• downward sloping demand for the individual firms but more elastic since there are many substitutes and the demand (or P) is greater then the MR
• D=P>MR
• zero (normal) economic profits in long run equilibrium because of few barriers to entry so ATC is tangent to the demand curve
• quantity produced is where MR=MC (Qmc)
• productive efficiency is NOT achieved
  • equilibrium quantity (Qmc) is NOT where ATC is at a minimum (P>minimum ATC)
  • they do NOT produce the quantity where MC=,ATC
  • at the profit maximizing level of output ATC is higher than the minimum
• allocative efficiency is NOT achieved
  • equilibrium quantity (Qmc) is NOT at the quantity where P=MC
  • at the profit maximizing level of output (Qmc), P>MC
  • meaning that there is an underallocation of resources; too little is being produced
  • as long as firms have some market power (i.e. the demand is downward sloping) they will maximize profits by producing a quantity that is less than the socially optimal quantity (Qso)

  

Summary

• imperfect competition (monopoly, monopolistic competition, and oligopoly) is a form of market failure; the market fails to achieve efficiency as we saw in this lesson
• ME: we studied market failure when we studied externalities in chapter 5; when externalities exists markets fail to achieve efficiency
• ME: in chapter 2 where we studied the economic functions of government, one of the functions was to try to maintain competition ;i.e. to correct markets when they fail to achieve efficiency; we also studied this in chapter 18 when we discussed antitrust laws and monopoly regulation
• since most industries are imperfectly competitive, does this mean that the most markets are market failures?
  • if we just look at the graphs we would have to answer "yes", "technically speaking"
  • but there are also some benefits to imperfectly competitive markets that also have to be considered:
    • the great degree of product differentiation provides society with a lot of benefits that may make up for some of the underallocation of resources (customer service, innovation, product development); variety is good